José Goossen Karssenberg Islamitische Meetkundige Patronen
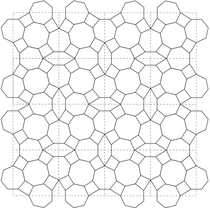
Een bijzondere tegelset
Deze tegelset heb ik bedacht om te gebruiken in een vraag van de Nationale Wetenschapsquiz 2014.
De vraag luidde: Wat kun je zeggen over de verhouding tussen de aantallen strikjestegels (links) en bootjestegels (rechts) wanneer een heel groot vlak zonder overlappingen en openingen bedekt wordt met deze tegeltjes?
Op de onderstaande foto zie je hoe in de uitzending wordt uitgelegd welke regelmaat er in het patroon zit.
Door de inkepingen en uitstulpingen kunnen de tegels namelijk maar op één manier een patroon vormen. Dit patroon heeft geen regelmaat zoals je meestal ziet, namelijk een regelmaat waarbij je, door het patroon 'over zichzelf' te verschuiven, je deze weer precies kan laten samenvallen met zichzelf. Dit heet translatie-symmetrie. Deze soort symmetrie is bij deze twee tegels onmogelijk.
Ondanks dat, is het toch mogelijk om een gigantisch groot vlak te bedekken met deze tegeltjes. Dit gaat door middel van de zogenaamde inflatie. Dit is een iteratieproces dat lijkt op het proces waarmee fractals worden gemaakt. De twee tegelvormen zijn namelijk in het groot te vormen met de oorspronkelijke tegels. Een grotere boot kun je samenstellen uit twee hele bootjes, zes halve bootjes en drie strikjes, zie hieronder links. Een grotere strik kun je maken met twee strikjes en zes halve bootjes.
Het bijzondere is, dat je dit proces eindeloos kunt herhalen: Met de grotere boten en strikken kun je nóg grotere boten en strikken vormen, waarbij de halve bootjes keurig op elkaar aansluiten en zo hele bootjes opleveren. Met die nóg grotere boten en strikken kunnen nóg grotere gigaboten en strikken gelegd worden en met deze gigaboten en strikken nóg weer grotere megaboten enstrikken enzovoort enzovoort.
Met eenvoudige matrixrekening kun je in dit iteratieproces telkens de aantallen strikjes en bootjes berekenen.
In het schema hieronder zie je hoe de aantallen bij elke stap groter worden wanneer je begint met één strik en twee boten die tegen elkaar aan liggen.
|
Start |
1e opdeling |
Totaal na eerste opdeling |
De 8 strikjes en 13 bootjes geven bij 2e opdeling |
Totaal na tweede opdeling |
De 55 strikjes en 89 bootjes geven bij 3e opdeling |
Totaal na derde opdeling |
|
1 strik |
2 strikjes, 3 bootjes |
2 + 6 = 8 strikjes |
16 strikjes, 24 bootjes |
16 + 39 = 55 strikjes |
110 strikjes, 165 bootjes |
110 + 267 = 377 strikjes |
|
2 boten |
6 strikjes, 10 bootjes |
3 + 10 = 13 bootjes |
39 strikjes, 65 bootjes |
24 + 65 = 89 bootjes |
267 strikjes, 445 bootjes |
165 + 445 = 610 bootjes |
Deze totalen komen ook in de rij van Fibonacci voor (elk volgend getal is de optelling van de twee voorafgaande getallen):
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
Van deze rij is bekend dat de verhouding tussen twee opeenvolgende getallen steeds dichter naar de Gulden Snede verhouding nadert (die verhouding is, afgerond op drie decimalen, 1 staat tot 1,618).
Het verband tussen semiperiodieke betegelingen en islamitische mozaïeken
Dit type semiperiodieke betegelingen (of quasi-periodieke betegelingen) is eind jaren ’60 en in de jaren ’70 van de vorige eeuw ontdekt door met name Raphael Robinson en Roger Penrose.
De strikjestegel en de bootjestegel zonder inkepingen en uitstulpingen werden wel al vanaf de 11e eeuw of zelfs eerder in Perzië gebruikt om prachtige mozaïeken te ontwerpen. Ze dienden als zogenaamde prototegels of ‘Gireh-tegels’ (Het Perzische woord Gireh of Girih betekent ‘knoop’). Kenmerkend voor deze tegels is, dat ze in het uiteindelijke mozaïek niet zichtbaar zijn. Maar ze geven wel de structuur van het gehele tableau aan.
In een artikel van Peter Lu en Paul Steinhardt (Science, feb 2007) wordt gesuggereerd dat men destijds ook bekend was met a-periodieke betegelingen. Hier is echter geen enkel bewijs voor. Het artikel van Lu en Steinhardt veroorzaakte een schandaal omdat het aperte onjuistheden bevatte en een misleidende verbinding legde tussen islamitische geometrische patronen en de Penrose-kites-and-darts-betegelingen. Ook verzuimden ze melding te maken van een reeds eerder gepubliceerd artikel van Emil Makovicky hierover.
Peter Cromwell corrigeerde Lu en Steinhardt in een artikel gepubliceerd in de Mathematical Intelligencer, 2008 .
Een opmerkelijke andere eigenschap van de twee tegelvormen is ook, dat een bootje een ϕ x zo grote oppervlakte heeft als een strikje. Dit betekent dat, wanneer je naar de oppervlakteverhouding van een betegeling van deze strikjes en bootjes kijkt, deze oppervlaktes zich verhouden als:
1 : ϕ-kwadraat, dit is ongeveer 1 : 2,618.
Gebruik van de tegelset in de islamitische wereld
In de islamitische wereld zijn de tegels zelf niet meer zichtbaar op mozaïeken, maar wel de lijnen die op de tegels getekend worden:
Dit detail uit een tableau in Qom, Iran (foto Prof. J. Hogendijk), toont de vliegers en andere vormen die dan ontstaan. Ook de regelmatige tienhoek is gebruikt als prototegel. Op die tienhoek wordt dan een tienpuntige ster getekend (op de foto van het mozaïek uit Qom zijn die linksboven en rechtsonder voor een kwart zichtbaar).
Er zijn talloze andere voorbeelden bekend van prachtige ornamenten.
Recent Activities, News
Workshopdagen Valuascollege Venlo juni 2024
Klik op de foto naar een verslag
Houten versie Geofractor
De plastic geofractor uit het boekje is nu ook verkrijgbaar in de houten variant. Prijs €12,50
Boekje in zebrareeks is half april 2023 verschenen.
Artikel in Euclides
Half maart 2023 is in het vakblad van wiskundeleraren een artikel van me verschenen naar aanleiding van de publicatie van Zebra 66 Islamitische Meetkundige Patronen
Recensie Snijpunt Isfahan
Lees hier
First prototype of new aperiodic puzzle
The developing process is continued. click here.
Ars et Mathesisdag 2019
During the art- and maths day (Ars et Mathesisdag), 24 november 2018, I gave a lecture about analyzing historical geometric patterns and trying to find new ones.
Timelapse construction
A great timelapse construction by Ameet Hindocha. More can be found on the website Ambigraph
Article online available
The journal For the Learning of Mathematics made my 2014 article 'Learning geometry by designing Persian mosaics' online available: See https://flm-journal.org/Articles/2E0CB6E94D76C79C2F341680D60F17.pdf
Een kritische recensie van Snijpunt Isfahan
Here you find my reflections on a very critical review of Snijpunt Isfahan by a mathematician (in Dutch)
March 30 2018 Lecture
Lecture in Dutch
Two new 'floral'patterns
24 March 2018
Based upon the famous Alhambra pattern with circle segments. Click on the picture below to go there
14 feb 2018 Event about 'Snijpunt Isfahan' at Spui25
Look here
Interview by Dolf Jansen
Dolf Jansen interviewed Maite and me (in Dutch) during the radio program 'Spijkers met Koppen', to hear and watch the interview, klick here
Interview by Coen Verbraak
Coen Verbraak interviewed Maite and me about Maite's book 'Snijpunt Isfahan' (in Dutch), to hear and watch the interview, klick here
Official opening of Museum Gallery RAT (Recomposed Art Texel)
May 13 2017 we celebrated the opening of our new location Burgwal 20 Den Burg. Here you find artwork composed with beachcombed materials by Maria Roelofsen and my design studio for making new pattern compositions based upon the Islamic design tradition. For further information also look at www.museumgalerierat.nl
A new floral design with worksheet. Click on the picture to find more information about the Khatai Flower.
March 24th 2017
Heart cloud sun
Workshop in Amsterdam
21 august 2016 11.30-13.00
In the Tropenmuseum I delivered a workshop on the Islamic design tradition of geometric patterns in Dutch, further information here
Floral designs
A new subject is being developed and information will be available on this website: floral designs. I started today with the lotus flower. Click on the lotus below to visit the right tab.
24th of March 2016
Colour Plates available (not any more since the exhibition ended)
Download my puzzle-/colour plates at this link of the Tropenmuseum Junior
Short story 'Spiral Figures'
I wrote a short story in Dutch about a child who draws spiral figures at the beach
Students finished newly developed lesson strand on Islamic mosaic design
Click on the picture below and check the two slide shows on the 2015 results.
The workshop I delivered in 2014 is online since Jan. 2015
A miraculous set of tiles
Patchwork by Marijke Maris-Baan
Heptagon construction
A method to construct a near-regular heptagon now published on this site
Result of drawing competition
6 July 2014. The drawing cmpetition was won by José Bradamonte.
Students finished mosaic design course
A group of about 20 students finished the lesson strand on Persian style mosaics in the beginning of may 2014. You can find some impressions of their activities here
View their endresults here
Result of pre-study
Article published
2014, March.
My article 'Learning Geometry by Designing Persian Mosaics' is published in issue nr. 100 (March 2014) of the Canadian journal 'For the Learning of Mathematics'.
At the flm-website you can find an Abstract.
Examples of basic patterns
New pattern design
Click on the picture below to find a series of patterns with octagons
Workshop 1&2 Feb. 2014
The workshop held on Texel was attended by 13 people in total. Among them: a furniture maker, a designer of lamps, quilters, painters and teachers. See the photo-impression of the workshop
Article in local newspaper Texel
This article (text and photo Pip Barnard) is about my fascination for Islamic geometrical ornamentation and how it can be used in (mathematics) education.
Article in Dutch newspaper
An article about the artwork by Maria Roelofsen and myself was published in the Dutch newspaper 'Reformatorisch Dagblad' on 30 december 2013. (Text Janneke van Reenen-Hak, Photo's Sjaak Verboom)
Publication in dutch magazine 'Experiment NL'
In this magazine on dutch Scientific research an article was published about my work. All those who have a subscription of 'Quest' received this magazine. Four pages with beautiful illustrations!
International workshop on Islamic geometric design Istanbul
At the Design Center of Istanbul a six-days congres was organized with lectures and workshops delivered by experts in this field. Incredibly inspiring!
Conference Isfahan, Iran
May 2013. A three day conference for mathematicians and artists on geometric Islamic patterns was held. Lots of inspiring workshops and lectures were delivered.
Workshop Leiden
Workshop for students, Institute for Studies of the Middle East, Leiden University, 27 march 2013
Contribution to piece of art
Lecture for maths teachers
During the conference for Maths teachers held december 18th 2012 at the Groningen University I gave a lecture about using islamic mosaics to teach geometry at all levels in secundary schools.
Article Published
June 2012.
In the review for Dutch mathematics teachers called 'Euclides' the article 'Designing Persian Mosaics in the Classroom. Students in the centre of a medieval design tradition' appeared (for the article in Dutch click here).
Maria completed 'the frog'
